本文共 2900 字,大约阅读时间需要 9 分钟。
1. 引言
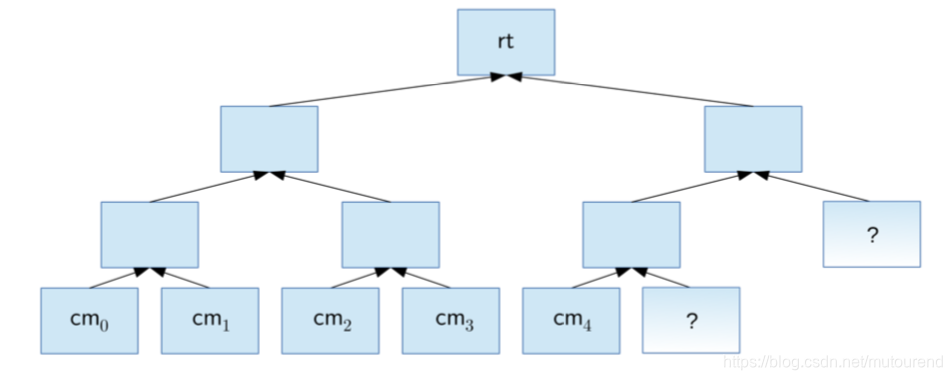
note commitment tree 与 Bitcoin中的unspent transaction output set (UTXO set) 的相同之处在于:
- 都可以express the existence of value and the capability to spend it。
note commitment tree 与 Bitcoin中的unspent transaction output set (UTXO set) 的不同之处在于:
- note commitment tree为append-only的,无法用其来防止双花。
note commitment tree的root 与 每个treestate 关联。
该incremental Merkle tree中的每个节点都与一个hash值关联,该hash值的长度为255-bit。
令root在0层,则在第 h h h层,有 2 h 2^h 2h个节点,编号为0~ 2 h − 1 2^h-1 2h−1。将 h h h层 i i i节点对应的hash值表示为 M i h M_i^h Mih。
所谓note position,是指:
the index of a note’s commitment at the leafmost layer。Merkle Tree Hash Function M e r k l e C R H S a p l i n g MerkleCRH^{Sapling} MerkleCRHSapling 用于对note commitment tree进行hash,其中:
- prefix l l l 用于区分inputs所在的layer。
- M e r k l e D e p t h S a p l i n g = 32 MerkleDepth^{Sapling}=32 MerkleDepthSapling=32
- l M e r k l e S a p l i n g = 255 l_{Merkle}^{Sapling}=255 lMerkleSapling=255

2. Merkle Path Validity
在incremental Merkle tree (note commitment tree) 中的每个节点都关联一个hash值,该hash值以bit sequence形式存在。
令root在0层,则在第 h h h层,有 2 h 2^h 2h个节点,编号为0~ 2 h − 1 2^h-1 2h−1。将 h h h层 i i i节点对应的hash值表示为 M i h M_i^h Mih。
在最底层,即 M e r k l e D e p t h S a p l i n g = 32 MerkleDepth^{Sapling}=32 MerkleDepthSapling=32,的节点称为leaf nodes。当添加一个note commitment到该tree中时,会在相邻可用的位置 i i i处添加leaf node hash value M i M e r k l e D e p t h M_i^{MerkleDepth} MiMerkleDepth。迄今未用的leaf nodes则关联 distinguished hash value U n c o m m i t t e d S a p l i n g = l 2 L E B S P l M e r k l e S a p l i n g ( 1 ) Uncommitted^{Sapling}=l2LEBSP_{l_{Merkle}^{Sapling}}(1) UncommittedSapling=l2LEBSPlMerkleSapling(1)。
从第0层至第 M e r k l e D e p t h S a p l i n g − 1 MerkleDepth^{Sapling}-1 MerkleDepthSapling−1层的所有节点都称为 internal nodes,这些节点都关联的值为 M e r k l e C R H S a p l i n g MerkleCRH^{Sapling} MerkleCRHSapling的输出。这些节点的值是基于其下一层的子节点计算的,即,for 0 ≤ h < M e r k l e D e p t h S a p l i n g 0\leq h< MerkleDepth^{Sapling} 0≤h<MerkleDepthSapling and 0 ≤ i < 2 h 0\leq i < 2^h 0≤i<2h,有:
M i h = M e r k l e C R H S a p l i n g ( M 2 i h + 1 , M 2 i + 1 h + 1 ) M_i^h=MerkleCRH^{Sapling}(M_{2i}^{h+1},M_{2i+1}^{h+1}) Mih=MerkleCRHSapling(M2ih+1,M2i+1h+1)在incremental Merkle tree (note commitment tree) 中,由 leaf node M i M e r k l e D e p t h M_i^{MerkleDepth} MiMerkleDepth 到 root M 0 0 M_0^0 M00 的 Merkle path为 序列值:
[ M s i b l i n g ( h , i ) h ] [M_{sibling(h,i)}^h] [Msibling(h,i)h] 其中 h h h的取值为由 M e r k l e D e p t h S a p l i n g MerkleDepth^{Sapling} MerkleDepthSapling到 1 1 1, s i b l i n g ( h , i ) = f l o o r ( i 2 M e r k l e D e p t h − h ) ⊕ 1 sibling(h,i)=floor(\frac{i}{2^{MerkleDepth-h}})\oplus 1 sibling(h,i)=floor(2MerkleDepth−hi)⊕1。若已知a Merkle path 和root r t = M 0 0 rt=M_0^0 rt=M00,可验证某 leaf node M i M e r k l e D e p t h M_{i}^{MerkleDepth} MiMerkleDepth 是否在该tree中。
3. Merkle path check

参考资料
[1]
转载地址:http://ckqx.baihongyu.com/